Конспект урока «РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХУРАВНЕНИЙ» по математике
УРОК ПО ТЕМЕ:
РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХУРАВНЕНИЙ.
(методическая разработка)
| | Разработала: БЕЛЯЕВАЛ.Г., преподаватель математики | |
| | | |
| | | |
| | | |
г. Анжеро – Судженс
Методическая цель: применения активных форм обучения на уроках математики.
Цели урока:
Образовательная: закрепить с учащимися основные приемы и методы решений логарифмических уравнений. Обеспечить овладение учащимися основными алгоритмическими приемами решения уравнений.
Воспитательная: воспитывать у учащихся аккуратность, внимание при выполнении записи и вычислений в тетрадях.
Развивающая: развить творческое, логическое и математическое мышление при решении уравнений, память.
Тип урока: урок обобщения и систематизации знаний.
Обеспечение урока: карточки-задания дифференцированного характера, таблицы с формулами.
Ход урока:
-
Организационный момент (3 мин.)
-
Устный счет (10 мин.)
-
Обобщение систематизация знаний (27 мин.)
-
Самостоятельная работа(35 мин.)
-
Подведение итога(5 мин.)
2. Устный счет: (игра- веер).
Учащиеся по очереди вытягивают примеры и устно решают, объясняя всему классу.
Примеры:
-
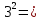
-
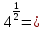
-
 =
= -
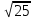 =
= -
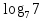 =
= -
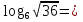
-
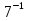 =
= -
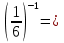
-
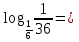
-
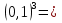
-
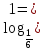
-
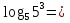
3. Обобщение и систематизация знаний:
Вопросы: 1. Какие уравнения называются логарифмическими?
2.Сколько существует методов решения логарифмических уравнений?
Вместе с учащимися на доске решаем примеры, записанные на доске указанными методами. Учащиеся
1 метод: Функционально – графический метод основан на использовании графических иллюстраций или каких-либо свойств функций.
(На листах будут решены графическим способом логарифмические уравнения и отдельно на листах будут изображены ответы. Нужно подобрать ответы к графикам функций).
2 метод: Метод потенцирования он основан на теореме
Теорема:
Логарифмическими уравнениями называются уравнения вида 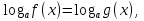 где a - положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
где a - положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
Примеры: а) 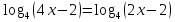
О.Д.З: 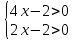 ;
; 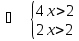 ;
; 
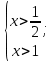
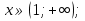
Потенцируем, т.е. освобождаемся от знаков логарифмов:

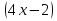 =
=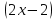 ;
;

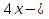
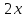 =
=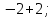
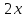 =
=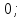
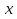 =
=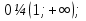
Ответ: корней нет.
3 метод: Метод введения новой переменной.
Пример: 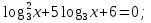 О.Д.З: x>0;
О.Д.З: x>0;
Введем новую переменную:
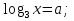
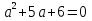 ;
;
D= 25 – 24=1;
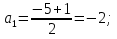
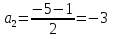 ;
;
Делаем обратную замену:
 ;
;
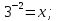
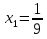 ;
;
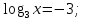
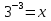 ;
;
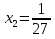 .
.
Ответ: 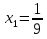 ;
; 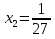 .
.
4 метод: Метод логарифмирования.
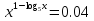 ;
;
Возьмем от обеих частей уравнения логарифмы по основанию 5, т.е. логарифмируем обе части уравнения:
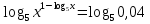 ;
;
(1-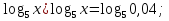
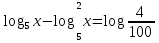 ;
;
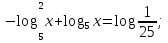
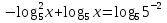 ;
;
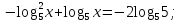
О.Д.З: x>0;
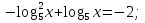
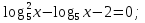
Введем новую переменную:
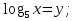
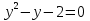 ;
;
D=1+8=9;
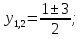
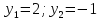 ;
;
Делаем обратную замену:
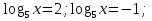
x=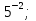 x=
x=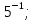
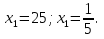

Ответ: 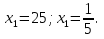
4. Самостоятельная работа по карточкам по вариантам:
1вариант:
-
Решите графически уравнение:
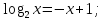
-
Решите уравнения: а)
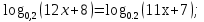
б) 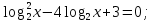
в) 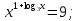
г) 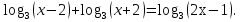
2 вариант:
-
Решите графически уравнение:
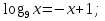
-
Решите уравнения: а)
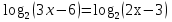 ;
;
б) 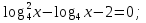
в) 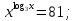
г) 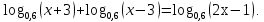
3 вариант:
-
Решите графически уравнение:
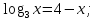
-
Решите уравнения: а)
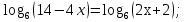
б) 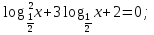
в) 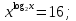
г) 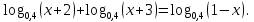
4 вариант:
-
Решите графически уравнение:
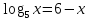 ;
; -
Решите уравнения: а)
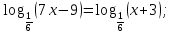
б) 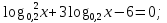
в) 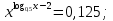
г) 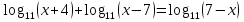 .
.
-
Подведение итога: выставление оценок и проверка самостоятельной работы.
-
Если осталось время:
Расшифруй фамилию известного путешественника, расположив ответы в порядке убывания. Чем он знаменит и в каком веке он жил?
-
Б
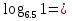
У
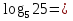
Л
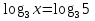
К
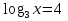
О
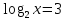
М
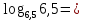
Здесь представлен конспект к уроку на тему «РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХУРАВНЕНИЙ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

