Конспект урока «Пирамида» по математике
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ № 28
Методическая разработка учебного занятия по математике по теме «Пирамида»
Преподаватель математики
ГАОУ СПО ТК №28
Медоева Л.Х.
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
учебного занятия по математике
ТЕМА: «Пирамида»
Профессия 260807.1 «Повар, кондитер»
Преподаватель высшей
квалификационной категории
Л.Х. Медоева
Москва 2013
«Стоит на земле пирамида, и боги о ней говорят.
На ней не рванье, не хламида, а вечного камня наряд». В.Я.Брюсов
План
учебного занятия по дисциплине «Математика»
Методическая цель – показать методику организации учебной деятельности в группах при проведении комбинированного занятия с применением информационно-коммуникационных технологий.
Тема занятия: «Пирамида».
Цели занятия:
-
Образовательные:
-
Познакомить с определением пирамиды, ее элементами, видами пирамид, основными формулами для вычисления площади пирамиды.
-
Научить применять полученные знания для решения задач с практической направленностью.
-
-
Развивающие:
-
развивать логическое мышление, умение сравнивать, сопоставлять;
-
формировать навыки самостоятельной работы в малых группах;
-
развивать рефлексивные навыки обучающихся, их математическую культуру и речь;
-
Воспитательные:
-
воспитывать умение контролировать свою деятельность и оценивать её;
-
формировать коммуникативные и информационные навыки, умение работать в команде
Тип занятия: усвоение и первичное закрепление новых знаний.
Вид занятия: комбинированный урок.
Оборудование:
-
мультимедиапроектор;
-
экран;
-
компьютер;
Методическое обеспечение: мультимедийная презентация, учебные пособия, учебники, технологическая карта обучающегося (задания, указания, рекомендации, критерии оценивания, листки рефлексии), диск «Геометрия 10-11» (виртуальный наставник), модели многогранников.
Литература:
-
А.В. Погорелов Геометрия 10-11.М: Просвещение , 2007.175с.;
-
В.С. Соломоник Сборник вопросов и задач по математике. М.: Высшая школа, 2006. 264с.;
-
О.А. Боковнев и др., Карточки-задания для программированного опроса по геометрии.
Интернет – ресурсы:
1.www.scool.edu.ru/dokedu.aspое
3Газета «Математика» издательского дома «Первое сентября» www.mat.september.ru
4.Математика в Открытом колледже www.mathematics.ru
-
Математика: консультационный центр преподавателей и выпускников МГУ www.school.msu.ru
-
Материалы по математике в Единой коллекции цифровых образовательных ресурсов
-
Образовательный математический сайт Exponenta.m htto://www.exponenta.ru
-
Общероссийский математический портал Math-Net.Ru www.mathnet.ru
-
Портал Alhnath.ni – вся математика в одном месте www.alhnath.ru
-
Виртуальная школа юного математика http://math.ournet.md
Ход урока:
-
Организационный момент (2 мин)
-
Актуализация опорных знаний (20 мин):
-
Индивидуальная работа по карточкам.
-
Фронтальный опрос по теме «Призма».
-
Изучение нового материала (25 мин)
-
Закрепление нового материала. Из истории пирамид
(35мин)
-
Домашнее задание (1 мин):
VI. Итоги занятия (7 мин),
-
Организационный момент. Слайд № 1. Приветствие, проверка готовности к уроку. Мотивация обучающихся на восприятие материала. Предлагается план учебного занятия Слайд № 2. Предложения от обучающихся по плану учебного занятия (обучающиеся разделены на 5групп)
-
Актуализация опорных знаний:
-
Фронтальный опрос по теме «Призма».
Фронтальный опрос по теме «Призма» (модели многогранников на столах у каждой группы, вопросы фронтального опроса)
1. Перед вами модели многогранников. Покажите многогранник, который мы изучали на предыдущих занятиях. Как он называется? (призма)
Сформулируйте определение призмы Слайд №3 (картинки призм)
-
Как обозначается призма?
-
Какие элементы призмы вы знаете?
-
Какие виды призм вы знаете? (прямая и правильная, выберите их из представленных моделей).
2. Сформулируйте определение прямой призмы, правильной.
3. Верно ли утверждение:
-
Любая прямая призма является правильной;
-
Любая правильная призма является прямой.
Ответ обоснуйте.
4. Алгоритм построения призмы;
-
Какие бывают призмы?
5. Сформулируйте определение параллелепипеда, перечислите его свойства;
-
Какие бывают параллелепипеды?
-
Чем отличается прямой параллелепипед от прямоугольного?
-
Какие свойства прямоугольного параллелепипеда вы знаете?
-
Чем отличается куб от прямоугольного параллелепипеда?
6. Из чего состоит поверхность призмы? Как можно вычислить площадь поверхности призмы? (формулы Sбок., Sполн.).
-
7. Боковое ребро наклонной треугольной призмы равно18см и образует с плоскостью основания угол 30
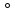 . Найдите высоту призмы.
. Найдите высоту призмы.
8. В правильной четырехугольной призме площадь основания равна
64 см 2, а боковое ребро 4см. Найдите диагональ призмы.
Группам отводится время на обсуждение ответов на вопросы. А в это время проверка индивидуальных заданий по карточкам. Затем ответы и комментарии групп. Оценивают работу группы и работу друг друга.
Итак, мы повторили:
1.Определение
2.Обозначение
3.Элементы
4.Построение
5.Виды
6.Свойства призм.
Сегодня на уроке все эти вопросы мы рассмотрим для многогранника, который называется пирамида – тема нашего занятия. Слайд №5.
III. Изучение нового материала.
Откройте тетради, запишите число и тему урока « Пирамида».
Кто может сформулировать цель нашего урока? Слайд №6 .
Этимологическая справка. Пирамида – слово произошло от названия формы хлебцев в Древней Греции – piros – рожь (пирог) или же от пламенеобразной формы пирамид pir – огонь. Еще одна гипотеза: греческое название piramis египетских пирамид произошло от выражения per me ous – боковое ребро сооружения. Апофема: греч. apothemа от apo – от, из и thema – приложенное, поставленное.
Каждой группе предлагается, сделав соответствующие записи в тетрадях, описать имеющуюся модель пирамиды по алгоритму Слайд №7:
1.Определение
2.Обозначение
3.Элементы
4.Построение
5.Вид
6.Свойства
Работа с учебником, дополнительной литературой.
Идет обсуждение вопросов. Учитель – в роли координатора – консультанта.
- Если основание пирамиды произвольный n- угольник, то пирамида - произвольная, если основание пирамиды правильный n- угольник, то пирамида - правильная.
-
Как вы считаете, какие условия должны выполняться, чтобы пирамида была правильной?
-
Основание - правильный многоугольник. Боковые ребра
перпендикулярны плоскости основания
-
Определение правильной пирамиды. Слайд №8
-
Какой многоугольник называется правильным?
-
Приведите примеры.
-
Что называется центром правильного многоугольника?
-
Где находится проекция вершины в правильной пирамиде? (в центре описанной окружности)
-
Где находится центр окружности, описанной около правильного треугольника? Слайд №9-11 (В точке пересечения медиан) (слайд построение правильной треугольной пирамиды, чертеж делают в тетрадях)
-
Учитель показывает модели правильных пирамид, просит показать основание, боковые ребра. Сравнить между собой боковые ребра. Доказать их равенство (из равенства прямоугольных треугольников: один катет общий, а другие катеты - радиусы окружности, описанной около основания).
-
Назвать боковые грани правильной пирамиды. Что можно о них сказать (они равные равнобедренные треугольники), докажите.
-
Предложить найти площади моделей пирамид. Затем переход на определение апофемы(Высота боковых граней правильной пирамиды) и ее обозначение l. Слайд №12.
-
Из чего складывается площадь полной поверхности пирамиды? (Sполн. = Sбок + Sосн.)
-
Из чего складывается площадь боковой поверхности? (запись формул в тетрадях и на доске).
IV.Закрепление изученного материала: (в каждой группе на столах есть и задания и вопросы на закрепление, группа сама выбирает и задает вопросы другим группами, комментирует их ответы)
Вопросы на закрепление (в виде мини-теста) обсуждаются группой, затем заслушиваются ответы представителей групп. Комментарии и оценка.
-
Сколько граней, вершин, ребер у n-угольной пирамиды?
-
Какое наименьшее число вершин, граней, ребер может иметь пирамида?
-
Высота пирамиды 3см. Чему равно расстояние от вершины пирамиды до плоскости основания?
-
Боковые ребра треугольной пирамиды равны 7см, 12см, 5см. Одно из них перпендикулярно к плоскости основания. Чему равна высота пирамиды?
-
Основание пирамиды четырехугольник, все стороны которого равны. Высота пирамиды проходит через точку пересечения диагоналей основания. Является ли данная пирамида правильной?
-
Всякий ли параллелограмм может быть основанием правильной пирамиды?
-
Верны ли утверждения:
-
Многогранник, одна из граней которого – правильный многоугольник, а остальные грани – четырехугольники, имеющие общую вершины, называется пирамидой.
-
Если основание пирамиды, произвольный многоугольник и вершина проецируется в центр этого многоугольника, то пирамида называется правильной.
-
Апофемой правильной пирамиды называется биссектриса ее боковой грани.
-
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на высоту пирамиды.
8. Приведите из своей будущей профессии пример изделий, имеющих форму пирамиды. Слайд №13-15
• Решение задачи профессиональной направленности. Обсуждение.
В рецептах всегда указывают, сколько грамм сахарной пудры требуется на посыпку поверхности кекса. Давайте разберем, как рассчитывают это количество.
Задача. Слайд №16. Рассчитайте, сколько грамм сахарной пудры потребуется на кекс, имеющий форму правильной четырехугольной пирамиды, если толщина слоя посыпки- 2мм, сторона основания 8см, длина бокового ребра 5см.
Решение.
m=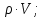 где m- масса
где m- масса
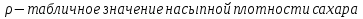 ,
, 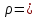 850
850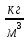
V – объем правильной 4-угольной призмы
V=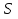 осн.
осн.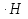 , где
, где  призмы, в нашем случае - толщина посыпки,
призмы, в нашем случае - толщина посыпки,
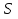 осн. – площадь боковой грани
осн. – площадь боковой грани
Из истории пирамид (презентация студентов)
V. Итоги занятия. Рефлексия (на партах есть листки рефлексии, листы контроля , которые заполняются обучающимися).
Лист контроля обучающегося
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | всего | |
| УЭ №1 | | | | | | | | | |
| УЭ №2 | | | | | | | - | - | |
| УЭ №3 | | | | | | | | | |
| Итого: | | | | | | | | | |
Критерии оценивания:
2 балла - задание выполнено верно;
1 балл - задания выполнено частично или с помощью консультанта;
0 баллов - задание не выполнено.
Перевод баллов в оценку: «5» - от 41 балла до 44
«4» - от 37 баллов до 40
«3» - от 18 баллов до 36
«2» - от 1 балла до 18
Лист рефлексии.
Перед вами система координат, в которой по 5-бальной системе оцените свою работу на занятии.
VI . Домашнее задание:
1. Подготовить презентацию или мини-сочинение на тему « Пирамида в нашей жизни и в моей будущей профессии»
2. Задание: построить пирамиду, основание которой прямоугольник, а вершина проецируется в центр описанной окружности.
3. А.В. Погорелов Геометрия 10-11, Стр.76, п.47-п.50, №41, №45. Слайд №17
4. См. лист рефлексии. Соедините точки (ваши оценки) и вычислите площадь полученной фигуры.
Здесь представлен конспект к уроку на тему «Пирамида», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
