Конспект урока «Разложение на множители с помощью формул квадрата суммы и квадрата разности» по математике для 7 класса
Тема: «Разложение на множители с помощью формул квадрата суммы и квадрата разности»
Тип урока: урок изучения нового материала.
Аннотация.
Урок разработан для учебника «Алгебра 7 класс»: учеб. для общеобразоват. учреждений (под редакцией С. А. Теляковского)- Москва: «Просвещение»,2010г.
Цель урока: получение и использование формул для возведения в квадрат суммы и разности выражений.
Задачи.
1. Обучающая: обеспечить усвоение материала всеми учащимися; учить и научить каждого ученика самостоятельно добывать знания; формировать навыки, умения, которые обеспечивают успешное выполнение деятельности.
2. Развивающая : способствовать развитию математического кругозора, мышления: умения анализировать, выделять главное, сравнивать, обобщать и систематизировать, развивать устную и письменную речи, внимание и память; продолжить работу по развитию умения самостоятельно приобретать новые знания; использование для достижения поставленной задачи уже полученных знаний.
3. Воспитывающая : содействовать воспитанию интереса к математике, активности, дисциплинированности, честности, ответственности за свой труд и труд одноклассника, воспитание навыков самоконтроля и взаимоконтроля.
Оборудование урока: учебник, карточки с заданиями, бланки ответов, тесты, формулы.
Этапы урока.
I. Opганизационный момент.
II. Актуализация знаний.
1) Игра «График».
2) Устные упражнения.
III. Усвоение новых знаний.
1) Подведение к новой теме (решение примеров).
2) Постановка проблемы и ее решение.
IV. Первичное закрепление новых знаний.
1) Игра «Открой окно»
2) Решение примера с комментированием.
Физкультминутка.
V. Закрепления новых знаний.
1) дидактическая игра в парах
2) историческая справка
3) тестирование (3 варианта – 3 уровня сложности)
4) самопроверка
VI. Домашнее задание.
VII. Рефлексия.
Содержание урока.
-
Opганизационный момент.
На доске эпиграф. «Математика- это полет». (В.Чкалов)
Взаимное приветствие; проверка подготовленности учащихся к уроку ; организация внимания.
-
Актуализация знаний.
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
Мы в поход отправляемся смело
В мир загадок и сложных задач.
-Начинается наше путешествие под названием «Покорители вершин». Наши вершины называются: «График», «Устные упражнения», «Новая тема», «Открой окно», «Расшифровка», «Тест».
-Итак, я предлагаю покорить первую вершину «График». В тетради вы фиксируете ответ только знаками: «да» ставится V, «нет» - ___. Рисуете график. Ответ проверяем по готовому образцу. В результате получается рисунок-график.(v-v-vv-vv).
Верны ли утверждения?
1)(–а)2 = а2 (да)
2) (2а)2 = 2а2 (нет)
3) (8)2 = 64 (да)
4) (–3х)2 =– 9х2 (нет)
5) ав + ва = 2ав (да)
6) (а + в)2 =) (а + в) )(а + в) (да)
7) –4а + 10а = 14а (нет)
8) 6cd – 10 cd = –4cd (да)
9) –7ху – 3ух = –10ху (да)
-Первая вершина «График» покорена.
- Покоряем следующую вершину «Устные упражнения».
-Устно выполните упражнения. –Замените квадрат произведением и упростите выражение.
1.52 = 5. 5 = 25
2.а2 = а. а
3.(5а)2 = 5а. 5а = 25а2
4.(2 + 3)2 = (2 + 3)(2 + 3) = 25
5.(а + в)2 = (а + в)( (а + в) = аа + ав + ва + вв = а2 + 2ав + в2
6.(х + у)2 = (х + у)(х + у) = хх + ху + ух + уу = х2 + 2ху + у2
- Какие закономерности видны в примерах 5и6?
III. Усвоение новых знаний.
-Обратите внимание на доску.
| II | III | |
| 1) (m + n)(m + n) = | = m2 + 2mn + n2 | = (m – n)2 |
Здесь записаны примеры в 3 столбца, 2 и 3 столбцы закрыты. Вы сейчас объединитесь в 3 группы и получите карточки с заданием: найти произведение данных многочленов, решите их, затем через некоторое время мы откроем 2 столбец.
Учащиеся находят произведение полученных многочленов. Работают по группам.
1группа: 1) (m + n)(m + n) =
2) (c + d)(c + d) =
2 группа: 3) (p + g)(p + g) =
4) (8 + m)(8 + m) =
3 группа: 5) (n + 5)(n + 5) =
6) (a + 3)(a + 3) =
Вопросы:
-Анализируем 2 столбец.
- Что явилось результатом умножения? (Трёхчлен)
1-й член – квадрат первого выражения
2-й член – удвоенное произведение 1 и 2 выражений
3-й член – квадрат второго выражения.
-Можно ли выражения в 1 столбце записать короче? (Открыть 3 столбец).
- Запишите общую формулу
(а+в)2 = а2 +2ав + в2
- А если возвести в квадрат (а – в)2, (в – а)2
- Что мы получим, если мы заменим в 1 и 3 столбцах знаки «+» на «–»?
- В каком месте стоит знак «–»?
-Запишите общую формулу
(а-б)2=а2-2аб+б2
- Изменится ли результат, если возвести в квадрат (–а – в)2?
(Мы знаем, что (–а)2 = а2, тогда (–а – в)2 = а2 + 2ав + в2 )
Подведём итоги. Как читается формула квадрата суммы ( разности) двух выражений? Вершина «Новая тема» покорена.
IV. Первичное закрепление новых знаний
-Я предлагаю решить № 799 (а, б); 800 (а, б) (1)в виде игры «Открой окно».
-Заполните пустые клетки, запишите примеры в тетрадях, предварительно проговорив.
1) Игра «Открой окно» № 799 (а, б);
а) (х + у)2 = х2 + 2х . у + ?2 = х2 + 2ху + у2
б) (р-q)2 = p2 – 2? + q2 = p2 – 2pq + q2
800(а, б)
а) (m+n)2 = m2 + ? mn + n2= m2 + 2mn +n2
б) (c-d)2 = ? - 2cd + d2 = c2 – 2cd + d2
2)Решение с комментарием.
№ 804 (а)
a) (7-8b)2 = 72 -2*7*8b + (8b)2=49-112b+64b2
-Вершина «Открой окно» покорена.
Физкультминутка.
а) Дыхательное упражнение
б) Упражнение для позвоночника
в) Упражнение для глаз
V. Закрепление новых знаний
1) Дидактическая игра в парах.
Вершина «Расшифровка»
-Некоторые из формул сокращенного умножения были известны ещё в древности. Эти формулы часто помогают при вычислениях. Каждая пара учеников должна решить свой пример. Найти в схеме букву, соответствующую ответу и поставить её под номером своей карточки. Полученное имя принадлежит известному математику, который с помощью формул сокращённого умножения доказал равенство (2а + в)2 = 4(а + в) а + в2
Примеры решают на местах в парах, помогая друг другу.
Карточки
1) (в2 + 2а2)2
3) (а2 – 3в)2
5) (а – 3в)2
2) (2в2 + 3а)2
4) (2а – 3в)2
6) (2в – 3а)2
Е) в4 – 4а2в2 – 4а2
Д) 4в2 – 12ав + 9а2
Л) 4а2 – 12ав + 9в2
К) а4 – 6а2в + 9 в2
И) а2 – 6aв + 9в2
В) 4в2 – 12в2а + 9а2
1 2 3 4 5 6
Е В К Л И Д
2) Историческая справка.
-Слово о Евклиде предоставляется одному из учащихся, подготовленному заранее.
Евклид – древнегреческий математик.
Автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения об Евклиде крайне скудны. Его научная деятельность протекала в Александрии в III в. до н.э. Евклид – первый математик Александрийской школы. Его главная работа «Начала» содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвёл итог предшествующему развитию греческой математики. Также Евклид – автор работ по астрономии, оптике, музыке и другим наукам. (Математика, Большой энциклопедический словарь М., Большая Российская энциклопедия, 1998 г.).
-Вершина «Расшифровка» покорена!
3) Мы подошли к следующей вершине «Тесты»
(Тестирование на 3 варианта – 3 уровня по степени сложности).
-Предлагаю вам тест (дифференцированный).
Выполнение:
1 варианта оценивается в 3 балла,
2 варианта оценивается в 4 балла,
3 варианта оценивается в 5 баллов.
-Выберитe себе вариант, внимательно прочитайте задание. К каждому заданию даны три ответа, из которых один верный. Решите задание, ответ запишите в бланк ответов, после мы сравним полученный ответ с предложенным.
I вариант
| Задания | Ответ | |||
| А | Б | В | ||
| 1) | (2а + в)2 | 2а2 + 2ав + в2 | 4а2 + 2ав + в2 | 4а2 + 4ав + в2 |
II вариант
| Задания | Ответ | |||
| А | Б | В | ||
| 1) | (с + 8)2 | с2 + 8с+ 16 | с2 – 16с + 64 | с2 + 16с + 64 |
III вариант
| Задания | Ответ | |||
| А | Б | В | ||
| 1) | (7у + 6)2 | 49у2 – 84у + 36 | 49у2 + 42у + 36 | 49y2 + 84y + 36 |
Бланк ответов
| № 1 | № 2 | № 3 | № 4 | |
| № ответа 1 в. |
|
|
|
|
| № ответа 2 в. |
|
|
|
|
| № ответа 3 в. |
|
|
|
|
Фамилия, имя:
Вариант:
В бланке ответов под номером задания поставьте букву в клеточке, которая cooтветствует выбранному ответу.
4) Самопроверка.
Ответы:
I вариант: В, Б, А.
II вариант: В, Б, А, Б.
III вариант В, Б, А, Б, В.
Перед самопроверкой учащиеся сдают бланки учителю, затем сверяют свои ответы и ставят себе оценки.
Вершина «Тесты» покорена!
VI. Домашнее задание.
-Доказать формулу (2а + в)2 = 4(а + в) а + в2 с помощью формулы квадрата суммы.
Пункт 32, выучить правила нахождения квадрата суммы и квадрата разности двух выражений. № 799(в, г); 800 (в, г); 803 (в, г); 804 (в, г).
VII. Рефлексия.
Путешествие подошло к концу.
-
Что нового мы узнали на уроке?
Пусть каждый из вас закончит фразу:
-Я научился..
-Я умею..
-Я сделаю..
-Вы все хорошо поработали. Спасибо за урок. Урок закончен.
Список литературы и интернет источников:
1.Учебник: Алгебра. 7 класс. Ю.Н. Макарычев, Н. Г. Миндюк и др. под редакцией С.А. Теляковского. - М.: Просвещение,-2010.
2. Методическое пособие: Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре для 7 класса. – М.: Илекса, – 2007.
3.www.planeta-kniga.ru
Тема : «Разложение многочленов на множители.»
Цель урока: показать различные приёмы разложения многочленов на множители и научить их применять.
Задачи:
-
научить использовать различные способы разложения;
-
развивать абстрактное и логическое мышление;
-
воспитание самостоятельности и самоконтроля.
Оборудование: персональный компьютер с мультимедийным проектором.
План урока:
-
Организационный момент.
-
Повторение (актуализация знаний учащихся: устная работа, самостоятельной работы с последующей проверкой через проектор). Слайд № 1, 2.
-
Выполнение упражнений по теме урока: Найди ошибку (слайд № 3). Исправь ошибку, самостоятельная работа (слайд № 4).
-
Изучение нового материала (слайд № 5).
-
Самостоятельная работа (слайд № 6).
-
Домашнее задание (слайд № 7).
1 этап
Проверяется подготовка детей к уроку.
2 этап
1.Представьте в виде квадрата одночлены: 81 m2 , 25x6,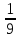 y14 , 0,04 x8
y14 , 0,04 x8
2.Преобразуйте трехчлен: x2+4x+4 9y+6y+1
A2-2A+1 m4-10m2+25
Демонстрируется 1 слайд, предлагается задание:
3.Распределите данные выражения по группам и объясните, по какому принципу.
-
3а2b(1-2a)
-
(x-2) (x2+2x+4)
-
27x6y3-72x4y4+48x2y5
-
(5a+1) 2
-
(9c-ab)(9c+ab)
-
ad -8a –bx+8x
-
kn-mn-n2+mk
-
x(x-4)(25+3x)
-
x4+4x3
-
-4a2+40ab-100b2
На выполнение задания дается 2-3 минуты. Далее учащиеся зачитывают результаты работы, проверка осуществляется через показ слайда № 2. На нем все выражения разбиты на 4 группы
1 группа
-
3а2b(1-2a)
-
(x-2)(x2+2x+4)
-
(5a+1)2
-
х (x - 4)(25 - 3x)
-
(9c-ab)(9c+ab)
2 группа
-
27x2y2 +72x2y2+48x2y5
-
-4a2+40ab-100b2
-
x4+4x3
3 группа
-
ad -8a –bx+8x
-
kn-mn-n2+mk
1 группа - произведения одночлена на многочлен или многочленов.
2 группа – многочлены, в которых есть общий числовой множитель.
3 группа – многочлены, разлагающиеся на множители способом группировки.
Учитель: Сформулируйте правила ,по которым можно сделать необходимые преобразования. (Ученики должны рассказать правила умножения одночлена на многочлен, умножения многочлена на многочлен, формулы квадрата суммы и квадрата разности, вынесения общего множителя за скобки)
3 этап
Учитель: Итак, цель нашего урока:Научиться раскладывать многочлены на множители тогда, когда обычные правила не помогают, и приходится применять сразу несколько различных способов (демонстрируется слайд № 3). Но сначала вспомним основные способы, уже известные нам. Выполним задание (слайд № 4).
Разложение с помощью формулы. Найдите ошибки в записях.
| Ошибочные записи | |
| (a-b) 2=a2-2ab+b2 | a-2ab+b a2-2ab+b2 a2-ab+b2 a2+2ab-b2 a2-2ab-b2 |
Учитель: Повторим формулу квадрата разности. А теперь закроем её. Объясните, какая ошибка допущена в каждой записи в правой части. (Во второй записи ошибки нет.)
Самостоятельная работа со взаимоконтролем. (Слайд № 5). На работу 2 минуты.
Исправьте ошибки в записях.
X2+y2-2xy=(x-y) 2
2•3•с-32-с2=(3-с) 2
m2+2mn - n2=(m-n) 2
2cb+c2+b2=(c+ b) 2
Для сильных учеников тест на компьютере.
После выполнения предложить учащимся поменяться тетрадями с соседом, и проверить работу товарища.
Учитель: Итак, главную формулу, изученную в этом году мы вспомнили, отработали и надеюсь ошибок в ней больше не будет.
4 этап
Учитель: А теперь будем применять для разложения на множители сложных многочленов различные способы. Кроме формул сокращенного умножения в этом нам поможет способ вынесения за скобки общего множителя. (Слайд № 6)
Способы вынесения общего множителя и группировки.
А•В+А•С=А • (В+С)
А•В-А•С=А • (В-С)
![]() =А • ( )+В • ( )=( ) •(А+В)
=А • ( )+В • ( )=( ) •(А+В)
Учитель: Первые две формулы мы умеем применять с 5-го класса. Впоследней применяется способ группировки слагаемых. Для этого слагаемые выбираются так, чтобы из каждой пары можно было вынести один и тот же общий множитель, который затем выносится за скобку. Это мы с вами тоже умеем.
Физкультминутка.
А теперь выполним упражнения.
Разложить на множители, используя различные методы. (Учащиеся по очереди выходят к доске и выполняют задания, записанные на ней в столбик)
5а3 -125 аb2=
a2 -2ab + b2 – ac + bc
63ab3 – 7a2b
m2 6mn + 9n2 – m -3m
2x2 + 4xy +4y2 -2x +1
7a2b -14ab2 + 7ab
b(a +c) +2a + 2c
x2 -3x – 5x + 15
Наводящие вопросы к заданиям:
1.Сколько слагаемых в сумме?
2. Есть ли у слагаемых общий множитель, который можно вынести за скобку?
3.Можно ли применить формулу квадрата суммы или разности двучлена, если слагаемых три?
4. Если слагаемых 4, то как их лучше сгруппировать?
-
этап
Выполнить самостоятельно. (Слайд № 7)
5р2-10рq+5q2
9-p2+q2-6q
m2-n2-8m+16
12z2-12z2+3z
m2-2n-m-4n2
A2+64b4
На работу отводится 7-10минут, выполняется она под копировку. После сдачи работы на проверку, демонстрируется слайд № 8с проверкой работы. Ученик и могут сразу оценить себя, посчитав верное количество ответов в работе. Задание, вызвавшее наибольшее затруднение может бать разобрано подробно.
6 этап
Домашнее задание задается на выбор: (слайд № 8)
№ 844 , 981 обязательное задание на оценку “3”.
№ 979,982 на оценку “4 и 5”.
Повторить все правила, используемые в теме.
Подведение итогов урока:
Оцените свою работу по карточке учета знаний.
1. Что нового узнали на уроке?
2. Удовлетворены ли вы своей работой?
Сколько ошибок допустили?
Здесь представлен конспект к уроку на тему «Разложение на множители с помощью формул квадрата суммы и квадрата разности», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (7 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

