Конспект урока «Многоугольники» по математике

Тема урока «Многоугольники».

Симоненко О.И., МОУ «Гимназия № 4» г. Саратов

Урок объяснения нового материала с использованием проблемного обучения.

Урок позволяет объяснить и закрепить новый материал.

Цель урока:

• изучить новый материал, используя знания, полученные раньше;

• научиться решать ключевые задачи по новой теме;

• формировать грамотную математическую речь; умение слушать, анализировать; делать;

• формировать интерес к предмету математики путём использования проблемного обучения, использования ИКТ;

• создать условия для развития творческих способностей и познавательной активности учащихся, содействовать развитию у школьников исследовательской культуры, помочь учащимся осознать ценность совместной работы.

Ход урока.

1. Постановка цели урока и мотивация учебной деятельности учащихся.

2. Объяснение нового материала.

   Вопросы учителя

   Ответы учеников
   Посмотрите на слайд, какие из данных фигур вы знаете? Что общего у всех фигур? Почему фигуры называются: треугольник, четырехугольник, пятиугольник и т.д. Можно ли данным фигурам дать одно общее название? Является ли треугольник многоугольником?	Прямоугольник, трапеция, параллелограмм, шестиугольник, треугольник Состоят из отрезков По количеству углов данных фигур Многоугольник Да
   Вспомните определение треугольника Какие элементы имеет треугольник? Назовите стороны и вершины. Что называется периметром треугольника?	Три точки, не лежащие на одной прямой, соединенные отрезками называются треугольником. Вершины, стороны Сумма длин всех сторон
   Запишем определение ломаной.
   Какие могут быть ломаные?	Выслушать различные ответы, а затем показать слайды. Замкнутые и незамкнутые
   Если звенья ломаной не пересекаются, не касаются и не совпадают, то такая ломаная называется простой.	Звенья ломаной могут пересекаться, касаться или совпадать. Ломаная без особенностей
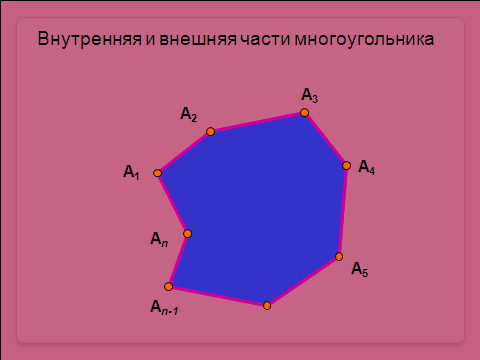
   Дайте определение многоугольника. Многоугольник - простая замкнутая ломаная вместе с частью плоскости, ограниченной ею.	Выслушать различные варианты
   Какие элементы есть у многоугольника? Как бы вы назвали вершины А1 и А2? Назовите все соседние вершины. Как бы вы назвали стороны А1А2 и А2А3? Назовите смежные стороны.	Вершины и стороны. Соседние Смежные
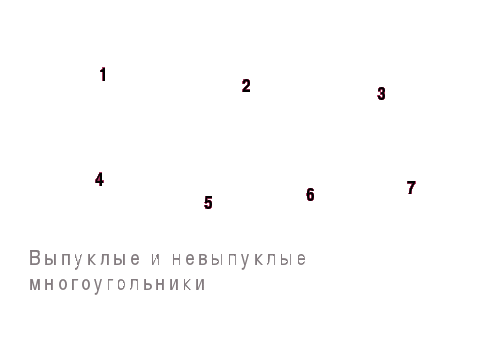
   Назовите выпуклые и невыпуклые многоугольники	Выпуклые: 1;4; 5;6 Невыпуклые: 2;3; 7
   Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Начертить в тетради многоугольники и провести прямые, проходящие через соседние вершины.
   Определение диагонали. Отрезок, соединяющий любые две несоседние вершины называется диагональю многоугольника. Начертите различные многоугольники и проведите из одной вершины диагонали. Назовите число сторон и число диагоналей. Кто заметил закономерность? Почему? А сколько при этом получилось треугольников? Чему равна сумма углов треугольника? Чему равна сумма углов выпуклого многоугольника.	Число диагоналей на три меньше числа сторон. Исходя из определения диагонали. Треугольников на 1 больше, чем диагоналей. 1800 1800(п-2)
   Вспомнить определение внешнего угла треугольника. Записать определение внешнего угла выпуклого многоугольника. Сколько внешних углов имеет выпуклый многоугольник? Чему равна сумма внутреннего и одного внешнего угла при вершине? Вычислите сумму всех внешних углов, взятых по одному около каждой вершины. Отметить, что сумма углов и сумма внешних углов многоугольника являются свойствами выпуклых многоугольников. Самостоятельно докажите следующий свойства выпуклых многоугольников: У выпуклого многоугольника все углы меньше 1800. Отрезок, соединяющий любые две точки выпуклого многоугольника, содержится в этом многоугольнике.	Внешний угол треугольника – угол, смежный с каким-нибудь углом этого треугольника. 2п 1800 3600

3. Проверочная работа.

Начертить многоугольник (для каждого ряда свой), обозначить его. Написать соседние вершины, смежные стороны. Найти сумму углов данного многоугольника.

4. Решение задач.

• Найдите сумму углов выпуклого 12-угольника. (1800⁰)

• Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 900⁰. (7)

• Определите сколько сторон имеет выпуклый многоугольник, если все его углы равны 120⁰? (6)

5. Постановка домашнего задания.

Выучить теоретический материал, доказать свойства выпуклых многоугольников, п.39, №364;367;369