Конспект урока «Арифметическая и геометрическая прогрессии» по математике
Тема урока:«Арифметическая и геометрическая прогрессии».
Цель урока:Систематизировать и обобщить знания учащихся по теме «Арифметическая и геометрическая прогрессии»
Задачи урока:
1. Образовательные: повторить теоретическую часть темы, проверить усвоение темы в ходе устной работы, индивидуальной и самостоятельной;
2. Развивающие: развивать интерес к предмету, познавательную активность, самостоятельность;
3. Воспитательные: развивать логику и речь учащихся; умение работать в группе, отстаивать свое мнение, принимать участие в диалоге, принимать точку зрения собеседника.
Тип урока:урок – обобщения и систематизации знаний.
Форма урока: групповая.
Ход урока
I . Организационный момент
1.Знакомство с целями и задачами урока.
2.Деление на группы класс разбивается на 2 группы (ученикам раздаются листочки с буквами d и q т.е. образуется команда разность и знаменатель).
II. Актуализация знаний
-
Конкурс на соответствие (проверка уровня математической подготовки по данному вопросу). Задается вопрос, группы должны поднять сигнальную карточку красного цвета, если ответ положительный или белую, если – отрицательный.
-
Сумма первого и второго членов геометрической прогрессии равна нулю, а произведение их равно 4. Можно ли задать такую геометрическую прогрессию? (нет)
-
Может ли сумма n первых членов арифметической прогрессии быть 0? (да)
-
Сумма первого и второго членов арифметической прогрессии равно 0, а частное их равно 1. Можно ли задать такую арифметическую прогрессию?(да).
-
Является ли последовательность (аn) - арифметической прогрессией, если равенство аn= аn-1 - аn+1/2 верно для любого n, большего 0?(да)
-
Может ли сумма nпервых членов геметрической прогрессии (g
 1) быть нулём? (нет)
1) быть нулём? (нет) -
Является ли последовательность bn геометрической прогрессией (n больше 1) bn2=bn-1
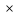 bn+1? (да)
bn+1? (да)
2.Творческое задание (индивидуальная) Цель задания: отрабатывать понимание математической речи на слух. На доске выписаны формулы, каждая со своим номером.
Учитель читает один раз любую из этих формул, а ученики на листочках записывают номер этой формулы. В конце задания получается число.(приложение 1 с формулами)
-
Свойство членов геометрической прогрессии. 7
-
Сумма бесконечной геометрической прогрессии(
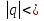 1). 5
1). 5 -
Сумма n первых членов геометрической прогрессии. 4
-
Свойство членов арифметической пргрессии. 6
-
N-й член арифметической прогрессии. 1
-
Сумма n первых членов арифметической прогрессии. 3
-
N-й член геометрической прогрессии. 2
Проверяют свои работы. Неверный ответ аккуратно одной чертой зачеркивают, ничего не исправляя. Проверка:7546132
Оценочная система: «0 ошибок» -5
«1 ошибка»-4
«2 ошибки»-3
III.Закрепление темы
1.Решение заданий.
На столе лежит конверт с заданиями, которые должны решить и составить фразу, используя таблицу.
(Решение заданий обсуждается. На доске записывается часть фразы).
Задания для команды d
-
Найдите семнадцатый член арифметической прогрессии: 19; 15;….
-
Найдите сумму первых семнадцати членов арифметической прогрессии: 19; 15;….
-
Найдите пятый член геометрической прогрессии
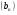 , если
, если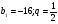 .
. -
Найдите сумму пяти первых членов геометрической прогрессии
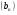 , если
, если 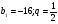 .
. -
-24; 12; -6;… - бесконечная геометрическая прогрессия. Найдите её сумму.
| ЛА | МА | ТИ | НИ | МА | КА | |
| -221 | 8 | - 45 | - 1 | 31 | - 31 | - 8 |
Задания для команды q
-
Найдите двадцать третий член арифметической прогрессии
 , если
, если 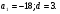
-
Найдите сумму первых двадцати трех членов арифметической прогрессии
 , если
, если 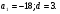
-
Найдите шестой член геометрической прогрессии
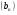 , если
, если 
-
Найдите сумму первых пяти членов геометрической прогрессии
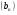 , если
, если 
-
– 48; 24; - 12;… - бесконечная геометрическая прогрессия. Найдите её сумму.
| ЦА | КО | ЦА | ЛУ | УК | НА | |
| 48 | 345 | 759 | - 62 | 96 | - 1 | - 32 |
Задания для команды d.
1. Найдите пятнадцатый член арифметической прогрессии  , если
, если 
2. Найдите сумму первых пятнадцати членов арифметической прогрессии  , если
, если 
3. Найдите пятый член геометрической прогрессии 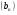 , если
, если 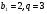 .
.
4. Найдите сумму первых пяти членов геометрической прогрессии 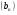 , если
, если 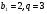 .
.
5. Найдите первый член бесконечной геометрической прогрессии, если  .
.
| РИФ | ДО | КА | МЕ | А | ЛЯ | |
| 14 | 525 | 26 | 162 | 242 | 12 | 98 |
Задания для команды q
1. Найдите сорок третий член арифметической прогрессии  , если
, если 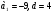 .
.
2. Найдите сумму первых сорока трех членов арифметической прогрессии  , если
, если 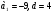 .
.
3.Найдите шестой член геометрической прогрессии 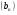 , если
, если 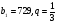
4.Найдите сумму первых шести членов геометрической прогрессии 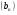 , если
, если 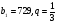 .
.
5.Найдите сумму бесконечной геометрической прогрессии: - 54; 18; - 6;… .
| ЛА | МА | КА | МА | КИ | ТИ | |
| 3225 | - 1092 | 159 | 1 | 3 | - 40,5 | 1092 |
-
«Думай,найди!»- прием «Автобусная остановка».
Определить какому виду последовательности относится
-
5;5,5;6;6,6;...... возрастающая
-
-9;-10,5;-12;-13,5....... убывающая
-
аn=3n-2 , аn=5n, аn=4n+6......... послед. задан. формулой
-
y1=-2, y2 =1, y3=0 , y4=1 , y5=2 , y6=3...... графический
-
0,0,0, .....;3,3,3.....;а,а,а..... реккурентный.
-
Тест ( выполняют в группе, потом проверяют друг у друга)
-
(аn) - арифметическая прогрессия. Найдите а4 , если а1=10, d= -0
1.9,7. 2. 97. 3.-97. 4. 10,3. 5. -10,3.
-
(bn) – геометрическая прогрессия. Найдите b6, если b1=4 и q=2.
1.-0,125. 2. 0,125. 3.1,25. 4. 12,5. 5. 1,25.
-
Найдите сумму бесконечной геометрической прогрессии: 12;6;......
1.6. 2. -12. 3.24. 4. -24. 5. 12.
-
Представьте в виде обыкновенной дроби число 0,(11).
1. 1.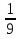 . 2. -9. 3.
. 2. -9. 3.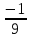 . 4.
. 4. 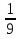 . 5. 9.
. 5. 9.
-
Найдите сумму ста первых членов последовательности (xn), если xn= 2n+1.
1. 20400. 2. 1200. 3.102. 4. 1020. 5. 10200.
IV. Рефлексия.Подведение итогов урока
Выставление оценок.Учащиеся анализируют свою работу на уроке, обсуждают, высказывают свое мнение, заполняют листы оценивания.
«Картинная галерея». На стикерах пишут отзывы об уроке и распологают их в одной из следующих строк на доске:
-
Оцените степень сложности урока.
Вам было на уроке:
-легко; -обычно; -трудно;
-
Оцените степень вашего усвоения материала:
-усвоил полностью; -усвоил частично;
-могу применить; -не усвоил
Оценочный лист
Группа___ Тема «Арифметическая и геометрическая прогрессии».
| Формативное | Суммативное | |||||
| Ф.И. ученика | соответствие | творческое задание | Решение задании | «Думай, найди» | тест | Итоговая оценка |
| | | | | | | |
Прилежание
Формулы
-
an = a1 + d(n - 1)
-
bn = b1qn – 1
-
Sn
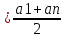 ∙n =
∙n =  ∙n
∙n -
Sn =
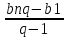 =
= 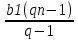 (q ≠ 1)
(q ≠ 1) -
S =
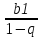 (
(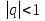 )
) -
an =
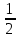 (an–1 + an + 1)
(an–1 + an + 1) -
b2n = bn-1 ∙ bn+1
Здесь представлен конспект к уроку на тему «Арифметическая и геометрическая прогрессии», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

