Циклоидальные кривые

Оглавление

Введение

В элементарной школьной геометрии рассматриваются прямые линии, отрезки прямых линий, ломаные линии, составленные из отрезков и некоторые кривые линии. Каждый вид кривых линий. определяется тем или иным специальным способом (например, окружность определяется как геометрическое место точек, имеющих заданное расстояние R от заданной точки О — центра окружности). В школьных учебниках дают определение линии, как границы куска поверхности (поверхность определяется при этом как граница тела) или как траектории движущейся точки. Но в рамках элементарной геометрии эти определения не получают отчётливой формулировки.

Циклоида (от греч. κυκλοειδής — круглый) — плоская трансцендентная кривая, которую можно определить как траекторию точки, лежащей на границе круга, катящегося без скольжения по прямой. Эту окружность называют порождающей.

1. Кривые.

Кривая или линия — геометрическое понятие, определяемое в разных разделах геометрии различно.

КРИВАЯ (линия), след, оставленный движущейся точкой или телом. Обычно кривую представляют лишь как плавно изгибающуюся линию, вроде параболы или окружности. Но математическое понятие кривой охватывает и прямую, и фигуры, составленные из отрезков прямых, например, треугольник или квадрат.

Кривые можно разделить на плоские и пространственные. Плоская кривая, например, парабола или прямая, образуется при пересечении двух плоскостей или плоскости и тела и поэтому целиком лежит в одной плоскости. Пространственную кривую, например, винтовую линию, имеющую форму спиральной пружины, нельзя получить как пересечение какой-нибудь поверхности или тела с плоскостью, и она не лежит в одной плоскости. Кривые можно также подразделить на замкнутые и открытые. Замкнутая кривая, например квадрат или окружность, не имеет концов, т.е. движущаяся точка, порождающая такую кривую, периодически повторяет свой путь.

Кривая есть геометрическое место, или множество, точек, удовлетворяющих некоторому математическому условию или уравнению.

Например, окружность – это геометрическое место точек плоскости, равноудаленных от данной точки. Кривые, определяемые алгебраическими уравнениями, называются алгебраическими кривыми.

Например, уравнение прямой y = mx + b, где m – угловой коэффициент, а b – отрезок, отсекаемый на оси y, – алгебраическое.

Кривые, уравнения которых содержат трансцендентные функции, например, логарифмы или тригонометрические функции, называются трансцендентными кривыми.

Например, y = log x и y = tg x – уравнения трансцендентных кривых.

Форму алгебраической кривой можно определить по степени ее уравнения, которая совпадает с наивысшей степенью членов уравнения.

• Если уравнение первой степени, например Ax + By + C = 0, то кривая имеет форму прямой.

• Если уравнение второй степени, например,

Ax² + By + C = 0 или Ax² + By² + C = 0, то кривая квадратична, т.е. представляет собой одно из конических сечений; к числу таких кривых относятся параболы, гиперболы, эллипсы и окружности.

Перечислим общие формы уравнений конических сечений:

• x² + y² = r² - окружность,

• x²/a² + y²/b² = 1 - эллипс,

• y = ax² - парабола,

• x²/a² – y²/b² = 1 - гипербола.

Кривые, соответствующие уравнениям третьей, четвертой, пятой, шестой и т.д. степеней, называются кривыми третьего, четвертого, пятого, шестого и т.д. порядка. Как правило, чем выше степень уравнения, тем больше изгибов будет у открытой кривой.

Многие сложные кривые получили специальные наименования.

• Циклоидой называется плоская кривая, описываемая фиксированной точкой окружности, катящейся по прямой, называемой образующей циклоиды; циклоида состоит из серии повторяющихся дуг.

• Эпициклоида – это плоская кривая, описываемая фиксированной точкой окружности, катящейся по другой неподвижной окружности вне ее.

• Гипоциклоидой называется плоская кривая, описываемая фиксированной точкой окружности, катящейся изнутри по неподвижной окружности.

• Спиралью называется плоская кривая, которая виток за витком раскручивается от неподвижной точки (или накручивается на нее).

Математики занимались изучением свойств кривых с глубокой древности, и названия многих необычных кривых связаны с именами тех, кто впервые их исследовал. Таковы, например, спираль Архимеда, локон Аньези, циссоида Диоклеса, кохоида Никомеда и лемниската Бернулли.

В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки и иногда определяется как «длина без ширины» или как «граница фигуры». По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и также трансцендентные кривые), применяя в каждом случае специальные приёмы.

Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:

При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [a,b] = [0,1], путями.

Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

и

эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h из отрезка [a₁,b₁] на отрезок [a₂,b₂], такая что

Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.

Аналитические определения

В курсах аналитической геометрии доказывается, что среди линий, записываемых в декартовых прямоугольных (или даже в общих аффинных) координатах общим уравнением второй степени

Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = 0

(где хотя бы один из коэффициентов A, B, C отличен от нуля) встречаются лишь следующие восемь типов линий:

а) эллипс;

б) гипербола;

в) парабола (невырожденные кривые второго порядка);

г) пара пересекающихся прямых;

д) пара параллельных прямых;

е) пара совпавших прямых (одна прямая);

ж) одна точка (вырожденные линии второго порядка);

з) "линия", совсем не содержащая точек.

Обратно, любая линия каждого из указанных восьми типов записывается в декартовых прямоугольных координатах некоторым уравнением второго порядка. (В курсах аналитической геометрии обычно говорят о девяти (а не о восьми) типах конических сечений, поскольку там различают "мнимый эллипс" и "пару мнимых параллельных прямых", - геометрически эти "линии" одинаковы, поскольку обе не содержат ни одной точки, но аналитически они записываются разными уравнениями.) Поэтому (вырожденные и невырожденные) конические сечения можно определить также как линии второго порядка.

В аналитической геометрии кривая на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y) = 0. При этом на функцию F накладываются ограничения, которые гарантируют, что это уравнение имеет бесконечное множество несовпадающих решений и

это множество решений не заполняет «куска плоскости».

Алгебраические кривые

Важный класс кривых составляют те, для которых функция F(x,y) есть многочлен от двух переменных. В этом случае кривая, определяемая уравнением F(x,y) = 0, называется алгебраической.

• Алгебраические кривые, задаваемые уравнением 1-й степени, суть прямые.

• Уравнение 2-й степени, имеющее бесконечное множество решений, определяет квадрики, то есть вырожденные и невырожденные конические сечения.

• Примеры кривых, задаваемых уравнениями 3-ей степени: циссоида Диокла, Декартов лист.

• Примеры кривых 4-ой степени: лемниската Бернулли и овал Кассини.

• Пример кривой 6-ой степени: астроида.

• Пример кривой, определяемой уравнением чётной степени: (многофокусная) лемниската.

Алгебраические кривые, определяемые уравнениями высших степеней, рассматриваются в алгебраической геометрии. При этом большую стройность приобретает их теория, если рассмотрение ведется на комплексной проективной плоскости. В этом случае алгебраическая кривая определяется уравнением вида

F(z₁,z₂,z₃) = 0,

где F — однородный многочлен трех переменных, являющихся проективными координатами точек.

Типы кривых

Плоская кривая — кривая, все точки которой лежат в одной плоскости.

Простая дуга(простая линия или жорданова дуга, также контур) — множество точек плоскости или пространства, находящихся во взаимно однозначном и взаимно непрерывном соответствии с отрезками прямой.

Путь — непрерывное отображение отрезка [0,1] в топологическое пространство.

Трансцендентная криваяаналитические кривые, не являющиеся алгебраическими. Более точно — кривые, которые можно задать через линию уровня аналитической функции (или, в многомерном случае, системы функций).

• Синусоида,

• Циклоида,

• Спираль Архимеда,

• Трактриса,

• Цепная линия,

• Гиперболическая спираль и др.

2. Способы задания кривых:

• аналитический – кривая задана математическим уравнением;

• графический – кривая задана визуально на носителе графической информации;

• табличный – кривая задана координатами последовательного ряда точек.

• параметрический (наиболее общий способ задать уравнение кривой) :

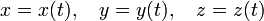
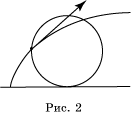
(1),

где  — гладкие функции параметра t, причем

(x')² + (y')² + (z')² > 0 (условие регулярности).

• Часто удобно использовать инвариантную и компактную запись уравнения кривой с помощью вектор-функции:

,

где в левой части стоит радиус-вектор точек кривой, а правая определяет его зависимость от некоторого параметра t. Раскрыв эту запись в координатах, мы получаем формулу (1).

3. Циклоида.

История исследования циклоиды связана с именами таких великих учёных, философов, математиков и физиков, как Аристотель, Птолемей, Галилей, Гюйгенс, Торричелли и др.

Циклоида (от греч. κυκλοειδής — круглый) — плоская трансцендентная кривая, которую можно определить как траекторию точки, лежащей на границе круга, катящегося без скольжения по прямой. Эту окружность называют порождающей.

Одним из древнейших способов образования кривых является кинематический способ, при котором кривая получается как траектория движения точки. Кривая, которая получается как траектория движения точки, закрепленной на окружности, катящейся без скольжения по прямой, по окруж­ности или другой кривой, называется циклоидальной, что в переводе с греческого языка означает кругообразная, напоминающая о круге.

Рассмотрим сначала случай, когда окружность катится по прямой. Кривая, которую описывает точка, закрепленная на окружности, катящейся без скольжения по прямой линии, называется циклоидой.

Пусть окружность радиуса R катится по прямой а. С – точка, закрепленная на окружности, в начальный момент времени находящаяся в по­ложении А (рис. 1). Отложим на прямой а отрезок АВ, равный длине окружности, т.е. АВ = 2 π R. Разделим этот отрезок на 8 равных частей точками А1, А2, ..., А8 = В.

Ясно, что когда окружность, катясь по прямой а, сделает один оборот, т.е. повернется на 360, то она займет положение (8), а точка С переместится из положения А в положение В.

Если окружность сделает половину полного оборота, т.е. повернется на 180, то она займет положение (4), а точка С переместится в самое верхнее положение С4.

Если окружность повернется на угол 45, то окружность переместится в положение (1), а точка С переместится в положение С1.

На рисунке 1 показаны также другие точки циклоиды, соответствующие оставшимся углам поворота окружности, кратным 45.

Соединяя плавной кривой построенные точки, получим участок циклоиды, соответствующий одному полному обороту окружности. При следующих оборотах будут получаться такие же участки, т.е. циклоида будет состоять из периодически повторяющегося участка, называемого аркой циклоиды.

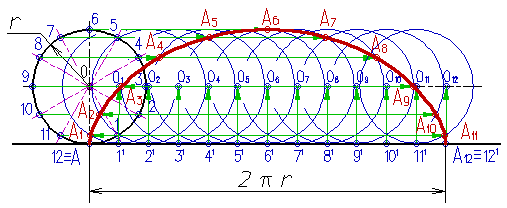
Обратим внимание на положение касательной к циклоиде (рис. 2). Если велосипедист едет по мокрой дороге, то оторвавшиеся от колеса капли будут лететь по касательной к циклоиде и при отсутствии щитков могут забрызгать спину велосипедиста.

Первым, кто стал изучать циклоиду, был Галилео Галилей (1564 – 1642). Он же придумал и ее название.

Свойства циклоиды:

1. Циклоида — периодическая функция по оси абсцисс, с периодом 2πr. За границы периода удобно принять особые точки (точки возврата) вида t = 2πk, где k — произвольное целое число.

2. Для проведения касательной к циклоиде в произвольной её точке A достаточно соединить эту точку с верхней точкой производящей окружности. Соединив A с нижней точкой производящей окружности, мы получим нормаль.

3. Длина арки циклоиды равна 8r. Это свойство открыл Кристофер Рен (1658).

4. Площадь под каждой аркой циклоиды втрое больше, чем площадь порождающего круга. Торричелли уверяет, что этот факт был открыт Галилеем.

5. Радиус кривизны у первой арки циклоиды равен .

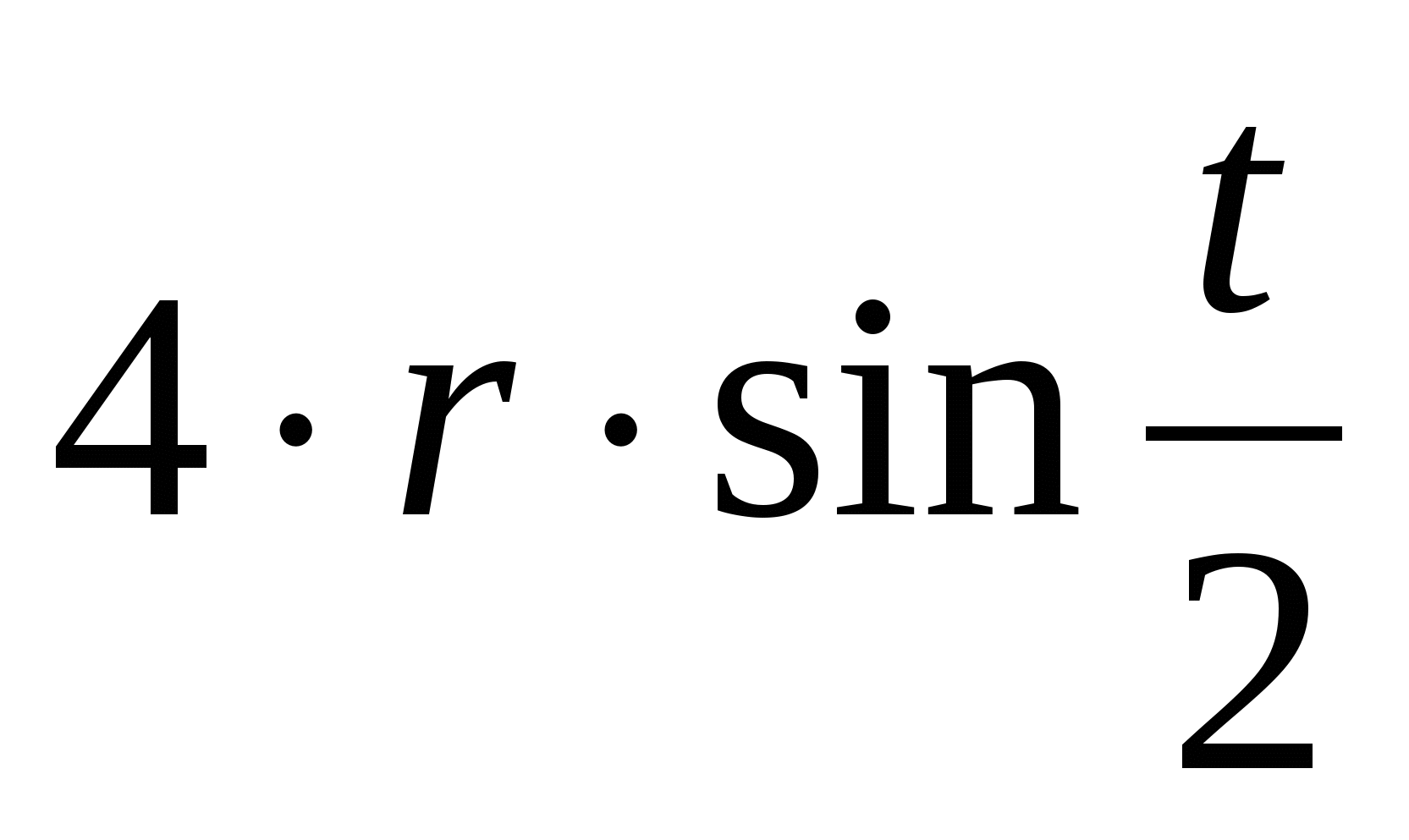
6. «Перевёрнутая» циклоида является кривой скорейшего спуска (брахистохроной). Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.

7. Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды, этот факт был использован Гюйгенсом для создания точных механических часов.

8. Эволюта циклоиды является циклоидой, конгруэнтной исходной, а именно — параллельно сдвинутой так, что вершины переходят в «острия».

9. Детали машин, которые совершают одновременно равномерное вращательное и поступательное движение, описывают циклоидальные кривые (циклоида, эпициклоида, гипоциклоида, трохоида, астроида) (ср. построение лемнискаты Бернулли).

Циклоида обладает целым рядом замечательных свойств. Упомянем о некоторых из них.

Свойство 1. (Ледяная гора.) В 1696 году И.Бернулли поставил задачу о нахождении кривой наискорейшего спуска, или, иначе говоря, задачу о том, какова должна быть форма ледяной горки, чтобы, скатываясь по ней, совершить путь из начальной точки А в конечную точку В за кратчайшее время (рис. 3, а). Искомую кривую назвали "брахистохроной", т.е. кривой кратчайшего времени.

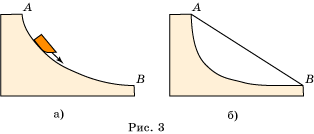
Ясно, что кратчайшим путем из точки A в точку B является отрезок AB. Однако при таком прямолинейном движении скорость набирается медленно и затраченное на спуск время оказывается большим (рис. 3, б).

Скорость набирается тем быстрее, чем круче спуск. Однако при крутом спуске удлиняется путь по кривой и тем самым увеличивается время его прохождения.

Среди математиков, решавших эту задачу, были: Г.Лейбниц, И.Ньютон, Г.Лопиталь и Я.Бернулли. Они доказали, что искомой кривой является перевернутая циклоида (рис. 3, а). Методы, развитые этими учеными при решении задачи о брахистохроне, положили начало новому направлению математики - вариационному исчислению.

Свойство 2. (Часы с маятником.) Часы с обычным маятником не могут идти точно, поскольку период колебаний маятника зависит от его амплитуды: чем больше амплитуда, тем больше период. Голландский ученый Христиан Гюйгенс (1629 – 1695) задался вопросом, по какой кривой должен двигаться шарик на нитке маятника, чтобы период его колебаний не зависел от амплитуды. Заметим, что в обычном маятнике кривой, по которой движется шарик, является окружность (рис. 4).

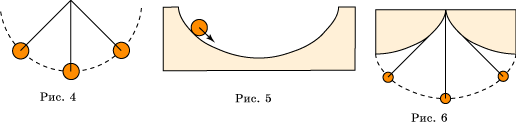
Искомой кривой оказалась перевернутая циклоида. Если, например, в форме перевернутой циклоиды изготовить желоб и пустить по нему шарик, то период движения шарика под действием силы тяжести не будет зависеть от начального его положения и от амплитуды (рис. 5). За это свойство циклоиду называют также "таутохрона" – кривая равных времен.

Гюйгенс изготовил две деревянные дощечки с краями в форме циклоиды, ограничивающие движение нити слева и справа (рис. 6). При этом сам шарик будет двигаться по перевернутой циклоиде и, таким образом, период его колебаний не будет зависеть от амплитуды.

Из этого свойства циклоиды, в частности следует, что независимо от того, с какого места ледяной горки в форме перевернутой циклоиды мы начнем спуск, на весь путь до конечной точки мы затратим одно и то же время.

Уравнение циклоиды

1.Уравнение циклоиды удобно записывать через α – угол поворота окружности, выраженный в радианах, заметим, что α также равняется пути, пройденному производящей окружностью по прямой.

x=rα – r sin α

y=r – r cos α

2.Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса r.

Циклоида описывается параметрическими уравнениями

x = rt – r sin t,

y = r – r cos t.

Уравнение в декартовых координатах:

Циклоида может быть получена как решение дифференциального уравнения:

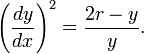
Из истории о циклоиде

Первым из учёных обратил внимание на циклоиду Николай Кузанский в XV веке, но серьёзное исследование этой кривой началось только в XVII веке.

Первым, кто стал изучать циклоиду, был Галилео Галилей (1564-1642) – знаменитый итальянский астроном, физик и просветитель. Он же придумал название «циклоида», что значит: «напоминающая о круге». Сам Галилей о циклоиде ничего не писал, но о его работах в этом направлении упоминают ученики и последователи Галилея: Вивиани, Торичелли и другие. Торичелли – известный физик, изобретатель барометра – уделял немало времени и математике. В эпоху Возрождения не было узких ученых-специалистов. Талантливый человек занимался и философией, и физикой, и математикой и всюду получал интересные результаты и делал крупные открытия. Немного позже итальянцев за циклоиду принялись французы, назвавшие её «рулеттой» или «трохоидой». В 1634 году Роберваль – изобретатель известной системы весов системы весов – вычислил площадь, ограниченную аркой циклоиды и её основанием. Содержательное исследование циклоиды провёл современник Галилея Мерсенн. Среди трансцендентных кривых, то есть кривых, уравнение которых не может быть записано в виде многочлена от x, y, циклоида — первая из исследуемых.

Паскаль писал о циклоиде:

Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса.

Новая кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали Декарт, Ферма, Ньютон, Лейбниц, братья Бернулли и другие корифеи науки XVII—XVIII веков. На циклоиде активно оттачивались методы появившегося в те годы математического анализа. Тот факт, что аналитическое исследование циклоиды оказалось столь же успешным, как и анализ алгебраических кривых, произвёл большое впечатление и стал важным аргументом в пользу «уравнения в правах» алгебраических и трансцендентных кривых. Эпициклоида

Некоторые виды циклоид

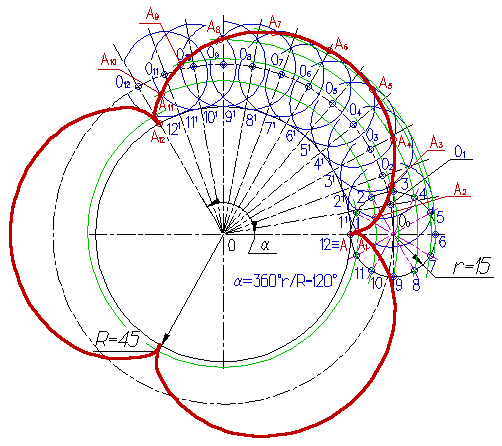
Эпициклоида - траектория точки А, лежащей на окружности диаметра D, которая катится без скольжения по направляющей окружности радиуса R (касание внешнее).

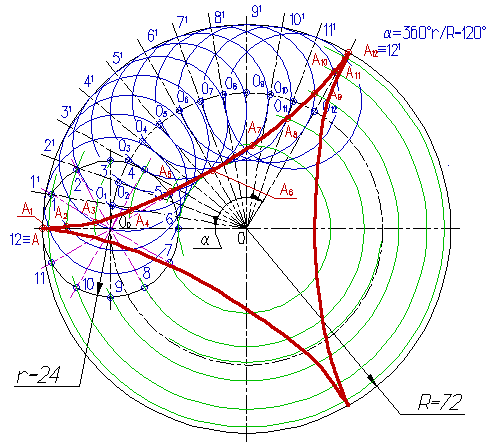
Построение эпициклоиды выполняется в следующей последовательности:

Производящую окружность радиуса r и направляющую окружность радиуса R проводят так, чтобы они касались в точке А;

Производящую окружность делят на 12 равных частей, получают точки 1, 2, ... 12;

Из центра 0 проводят вспомогательную дугу радиусом равным 000=R+r;

Центральный угол a определяют по формуле a =360r/R.

Делят дугу направляющей окружности, ограниченную углом a, на 12 равных частей, получают точки 11, 21, ...121;

Из центра 0 через точки 11, 21, ...121 проводят прямые до пересечения с вспомогательной дугой в точках 01, 02, ...012;

Из центра 0 проводят вспомогательные дуги через точки деления 1, 2, ... 12 производящей окружности;

Из точек 01, 02, ...012, как из центров, проводят окружности радиуса r до пересечения с вспомогательными дугами в точках А1, А2, ... А12, которые принадлежат эпициклоиде.

Гипоциклоида

Гипоциклоида - траектория точки А, лежащей на окружности диаметра D, которая катится без скольжения по направляющей окружности радиуса R (касание внутреннее).

Построение гипоциклоиды выполняется в следующей последовательности:

Производящую окружность радиуса r и направляющую окружность радиуса R проводят так, чтобы они касались в точке А;

Производящую окружность делят на 12 равных частей, получают точки 1, 2, ... 12;

Из центра 0 проводят вспомогательную дугу радиусом равным 000=R-r;

Центральный угол a определяют по формуле a =360r/R.

Делят дугу направляющей окружности, ограниченную углом a, на 12 равных частей, получают точки 11, 21, ...121;

Из центра 0 через точки 11, 21, ...121 проводят прямые до пересечения с вспомогательной дугой в точках 01, 02, ...012;

Из центра 0 проводят вспомогательные дуги через точки деления 1, 2, ... 12 производящей окружности;

Из точек 01, 02, ...012, как из центров, проводят окружности радиуса r до пересечения с вспомогательными дугами в точках А1, А2, ... А12, которые принадлежат гипоциклоиде.

4. Кардиоида.

Кардиоида (греч. καρδία — сердце, греч. εἶδος — вид) — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.

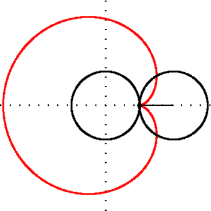
Кардиоида.

Кардиоида является частным случаем улитки Паскаля, эпициклоиды и синусоидальной спирали.

Кардиоида может быть также представлена как кривая, касающаяся всех окружностей, имеющих центы на данной окружности и проходящих через её фиксированную точку. Когда построены несколько таких окружностей, кардиоида оказывается построенной как бы сама собой.

Термин «кардиоида» введен Кастиллоном в 1741 году.

Если взять окружность и в качестве полюса точку на ней, то кардиоиду получим только в том случае, если откладывать отрезки, равные диаметру окружности. При других величинах откладываемых отрезков конхоидами будут удлиненные или укороченные кардиоиды. Эти удлиненные и укороченные кардиоиды называются иначе улитками Паскаля.

Кардиоида имеет различные применения в технике. В форме кардиоиды делают эксцентрики, кулачки у машин. Ею пользуются иногда при вычерчивании зубчатых колес. Кроме того, она применяется в оптической технике.

Свойства кардиоиды

Кардиоида — алгебраическая кривая четвёртого порядка.

Кардиоида имеет один касп.

Площадь фигуры, ограниченной кардиоидой, заданной формулой:

равна:

.

Уравнения кардиоиды

В прямоугольных координатах:

В прямоугольных координатах (параметрическая запись):

x = a cos t (1 + cost)

y = a sin t (1 + cost)

В полярных координатах:

Способы получения кардиоиды.

1)Если зафиксировать в плоскости некоторую окружность и начать катить по ней без скольжения другую окружность того же радиуса, то точка М на подвижной окружности будет описывать замкнутую траекторию. Эта плоская кривая называется кардиоидой.

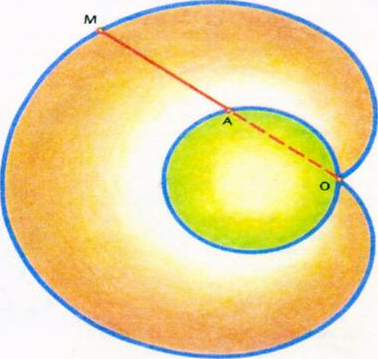
2)Кардиоиду можно получить и другим способом. Отметим на окружности точку О и проведем из нее луч. Если от точки А пересечения этого луча с окружностью отложить отрезок АМ, по длине равный диаметру окружности, и луч вращать вокруг точки О, то точка М будет двигаться по кардиоиде.

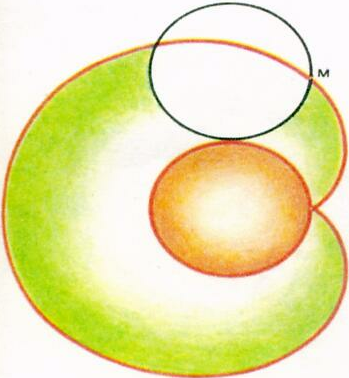
3)Кардиоида может быть также представлена как кривая, касающаяся всех окружностей, имеющих центры на данной окружности и проходящих через ее фиксированную точку. Когда построены несколько окружностей, кардиоида оказывается построенной как бы сама собой.

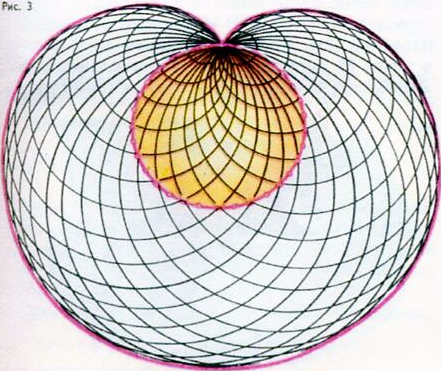
4)Есть еще столь же изящный, сколь, неожиданный способ увидеть кардиоиду. На рисунке можно увидеть точечный источник света на окружности. После того как лучи света отразятся в первый раз от окружности, они идут по касательной к кардиоиде. Представьте себе теперь, что окружность – это края чашки, в одной точке ее отражается яркая лампочка. В чашку налит черный кофе, позволяющий увидеть яркие отраженные лучи. Кардиоида в результате оказывается выделенной лучами света.

5. Астроида.

Астроида (от греч. astron — звезда и eidos — вид), плоская кривая, описываемая точкой окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. Принадлежит к гипоциклоидам. Астроида — алгебраическая кривая 6-го порядка.

Астроида.

Длина всей астроиды равна шести радиусам неподвижного круга, а площадь, ею ограниченная,- трем восьмым неподвижного круга.

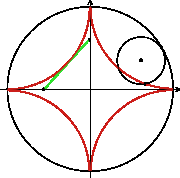
Отрезок касательной к астроиде, заключенный между двумя взаимно перпендикулярными радиусами неподвижного круга, проведенными в острия астроиды, равен радиусу неподвижного круга, независимо от того, как была выбрана точка.

Свойства астроиды

Имеются четыре каспа.

Длина дуги от точки с 0 до

Длина всей кривой 6R.

Радиус кривизны:

Площадь, ограниченная кривой:

Астроида является огибающей семейства отрезков постоянной длины, концы которых расположены на двух взаимно перпендикулярных прямых.

Астроида является алгебраической кривой 6-го порядка.

Уравнения астроиды

Уравнение в декартовых прямоугольных координатах:

| x | ^{2 / 3} + | y | ^{2 / 3} = R^{2 / 3}

параметрическое уравнение:

x = Rcos³t    y = Rsin³t

Способ построения астроиды

Чертим две взаимно перпендикулярные прямые и проводим ряд отрезков длиною R, концы которых лежат на этих прямых. На рисунке изображено 12 таких отрезков (включая отрезки самих взаимно перпендикулярных прямых). Чем больше проведем отрезков, тем точнее получим кривую. Построим теперь огибающую всех этих отрезков. Этой огибающей будет астроида.

6. Заключение

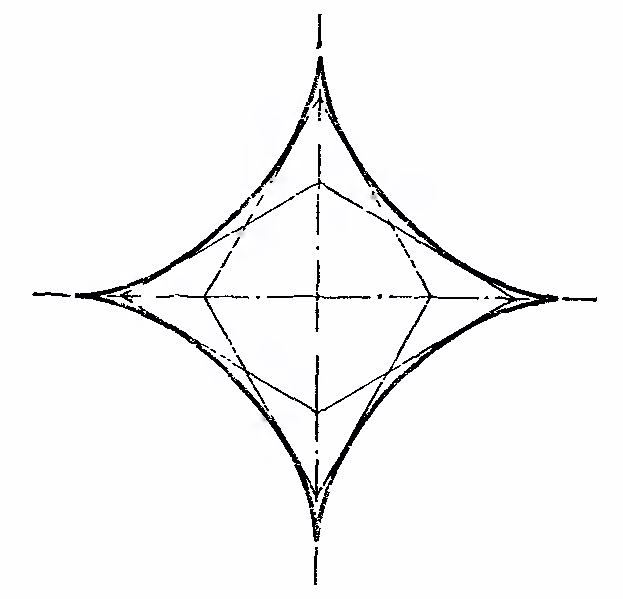
В работе приведены примеры задач с различными видами кривых, определяемых различными уравнениями или удовлетворяющих некоторому математическому условию. В частности циклоидальные кривые, способы их задания, различные способы построения, свойства этих кривых.

Свойства циклоидальных кривых очень часто используется в механике в зубчатых передачах, что существенно повышает прочность деталей в механизмах.

Список литературы

1. Г.Н. Берман «Циклоида».

2. Квант «Циклоида».

3. Энциклопедия для детей. Математика. Том 11.

4. Энциклопедия юного математика.

5. А.И. Маркушевич «Замечательные кривые».